节点高度变化的规律

如果一个节点的高度变化了一个单位，就可能会让父节点高度同样变化。（废话）

如果父节点的高度变化了，就关于父节点也考虑一下高度的变化。如果父节点的高度没变，就再也没有别的节点会改变高度了。（废话）

父节点高度不变有两种情况，一种是两棵子树始终平衡，并且较高的那棵高度没变；另一种是两棵子树不再平衡，父节点高度先是增加，不过我们用算法让两棵子树的高度“中和”了一下，让父节点的高度变回来了。

节点高度是从下到上开始考虑的，第一个改变高度的节点显然不会影响它的子节点。一个节点只有自己的高度改变了，才有可能改变父节点的高度（废话），所以所有改变高度的节点可以连成唯一的一条路径。因为重新平衡的算法一定会让不平衡点的高度恢复到原来的状态，而不平衡是由节点高度改变产生的，所以重新平衡只有可能出现在路径的末端。所以，一步插入、删除操作最多只需要对树进行一次重新平衡。

各种旋转

如果一棵树之前是平衡的，而现在不平衡了，既然一个插入/删除操作最多只会让节点的高度改变一个单位，说明这棵树的两棵子树原本就不一样高。有一棵子树比另一棵高一个单位，经历一步操作之后本来高的那棵又升高了一个单位，或者本来矮的那棵又降低了一个单位，树就不平衡了。

随便找个右子树原本就高一点，后面又升高了而导致不平衡的情况。圆圈表示节点，圆圈内部是节点的名字，右边表示节点的高度。A是需要重新平衡的节点，B、D和E的子树省略了，它们在这里不重要。这是插入新节点之前：

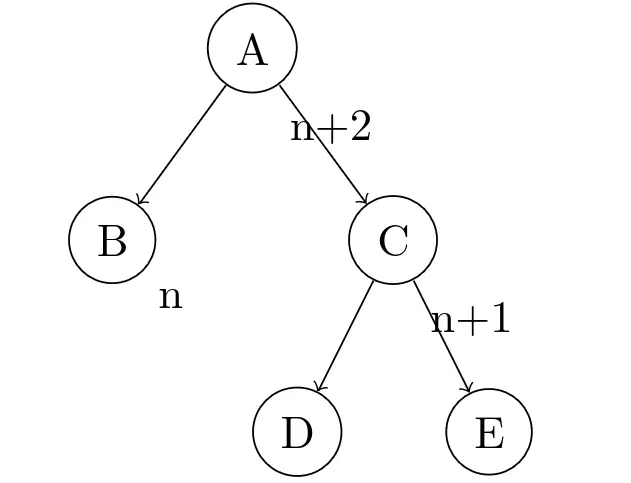
插入新节点之后，C又升高了一个单位。考虑到前面节点高度变化的规律，这里只有A两边是不平衡的，其他的都平衡。

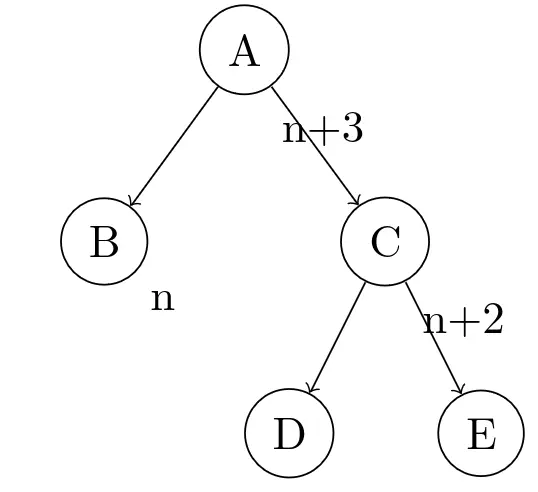
现在来考虑一下D和E的高度。C原本的高度是n+1，说明D和E里至少有一个高度为n，同时最低的那棵高度不能低于n-1。C的子节点要么高度都是n，要么有一个高度为n而另一个高度为n-1。不过第二种情况不可能发生，因为如果C的子节点高度不同，假设较矮的那棵子树升高了一个单位，C的高度就不会改变；如果较高的那棵升高了，C就不平衡了。这说明D和E原本是一样高的，只可能是n。

重新画一下插入新节点之前的图：

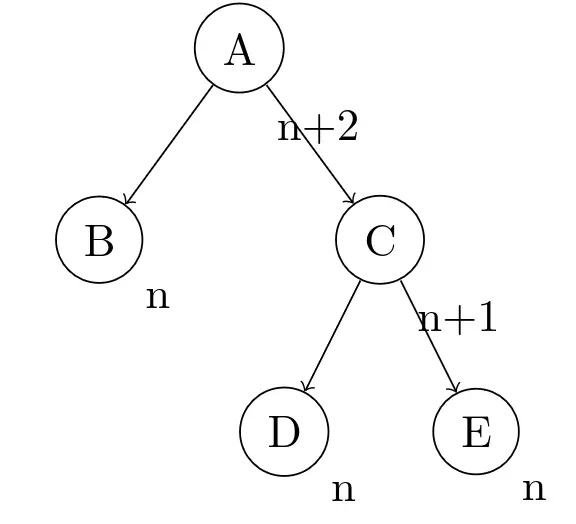
这时考虑插入节点后D和E的高度，就有两种情况了：

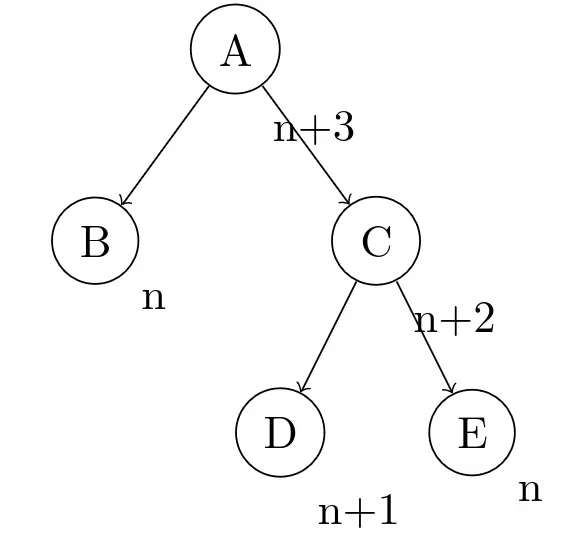
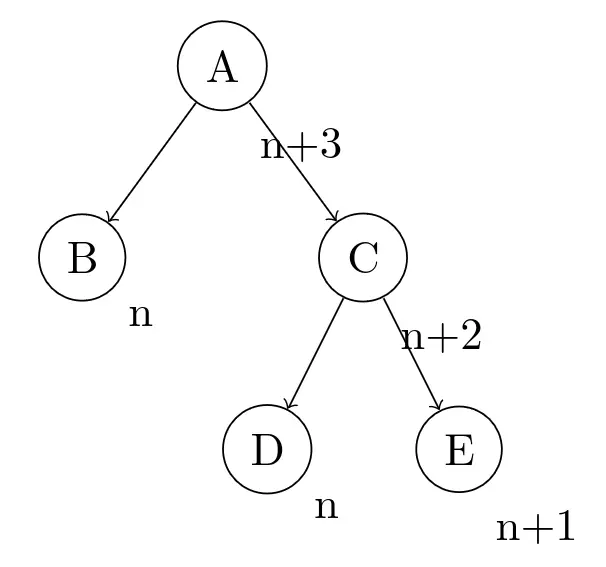
第二种情况处理起来比较简单。如果能改变这树的结构，让左子树升高一个单位，右子树降低一个单位，两边的树高变为n+1，树也就重新平衡了。这样处理还有一个好处，就是操作之后最高的节点高度为n+2，和插入新节点之前的一样，不会引起它父节点高度的变化，也就不用考虑后续平衡的问题了。

现在想让A成为左子树的一部分（为了让左子树升高一个单位），C不再是右子树的一部分（为了让右子树降低一个单位），就让C成为新的最高节点（暂且让我这么说吧，毕竟管它叫“根节点”不太好），让A变成C的左子树。为了在左边腾出空间，先让D变成游离的，之后往A变成子节点后空出的右边插就可以了。有点像让A和C绕着下方的一个点逆时针旋转一下，所以这个算法也叫“旋转”。

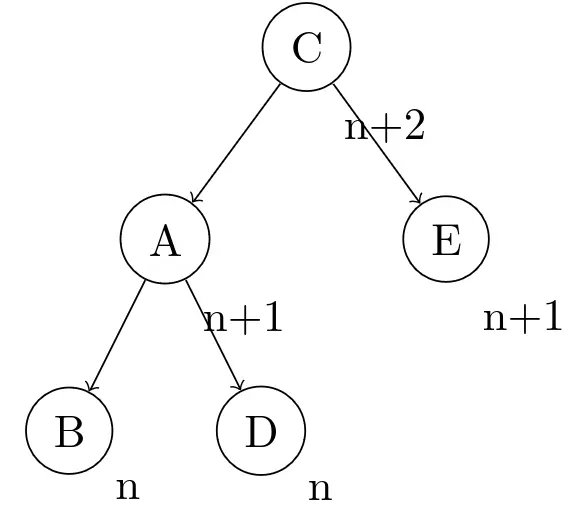
至于这样是叫左旋还是右旋，不同语言的书上不太一样。我的书上是 right-right，听起来有点反直觉，实际上是说不平衡是由A的右子树的右子节点升高引发的。

总结来说就是将C的左子节点设为A，然后将A的右子节点设为D。B < A < D < C < E，重新平衡之后的树也是符合二叉搜索树定义的。

现在我们已经能处理第二种不平衡的情况了，再来看下第一种。这个不平衡是由右子树的左子节点升高引发的：

要是还按第二种情况的方法操作（right-right 旋转），得到的树是这样：

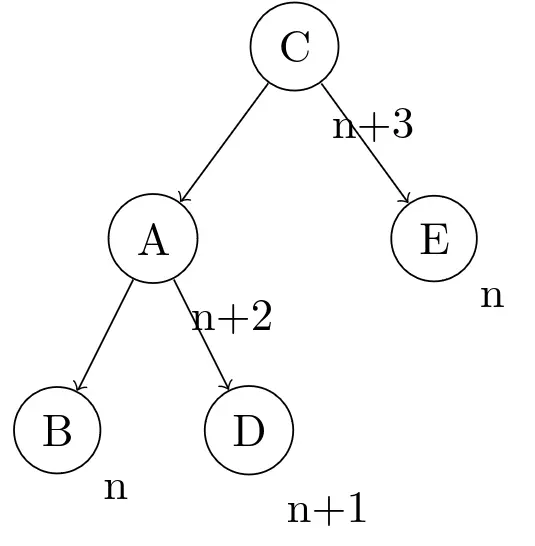
因为D的高度比B多一个单位，A的高度也要增加，树仍然是不平衡的。要是能把它变成 right-right 的情况，之后直接套用刚才的步骤就方便得多了。

重新观察一下 right-left 的树。要记得 right-left 的意思是，不平衡是由右子树的左节点升高而引发的：

这次先把右子树旋转一下，让右子树的右节点E比左节点D高就是了。要旋转右子树就需要考虑D的子节点的情况，把D的两个子节点标出来：

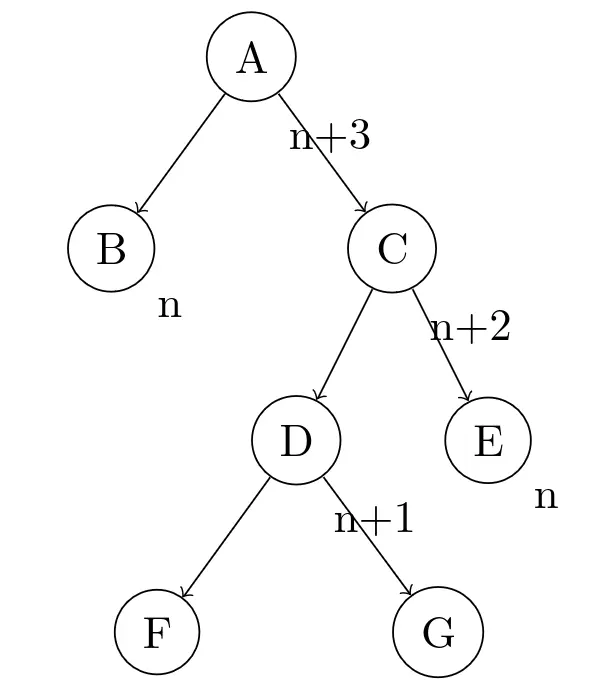
先让A的右节点Cleft-left 旋转一下：

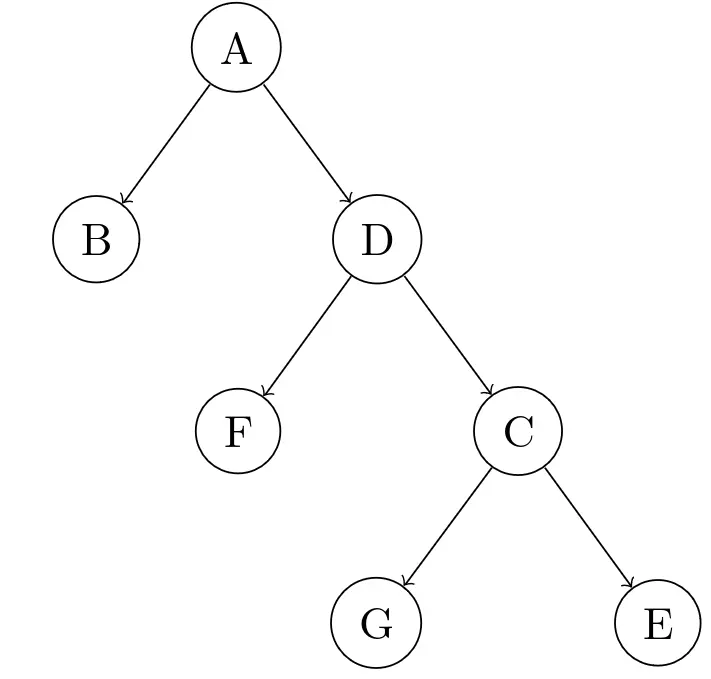
再让Aright-right 转一下就好了：

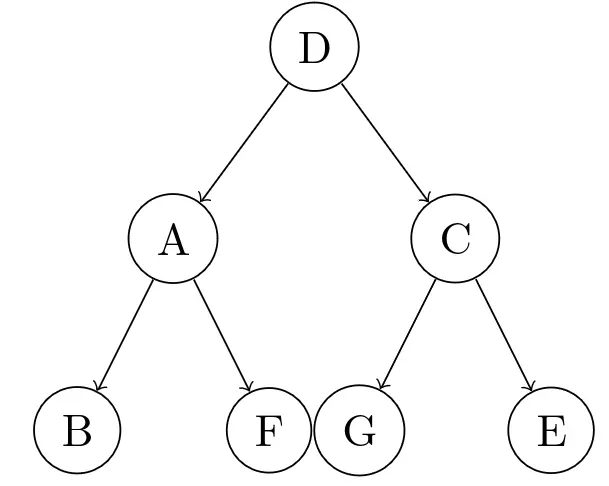
至于F和G的高度，用类似刚才分析C子节点高度的方法分析一下，D的子节点也是一个n一个n-1。我们没动B和E的子节点，所以它俩仍然是n。

算下无论F和G哪个是n哪个是n-1，树都是平衡的：

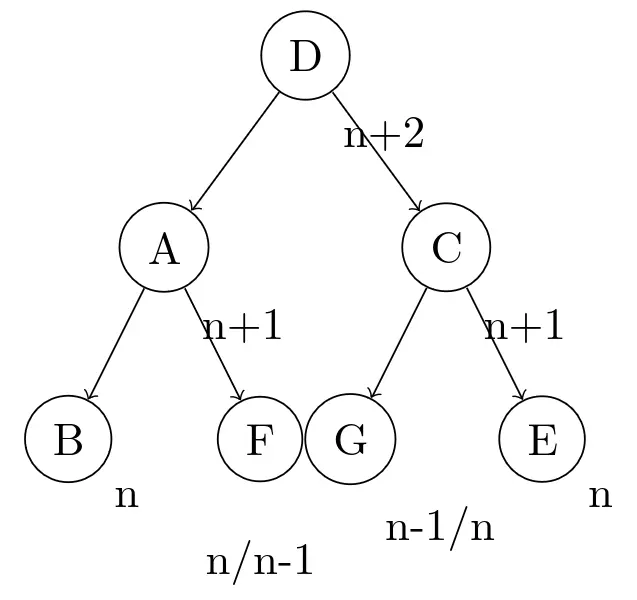
（若是你用F = n-1和G = n的情况考虑一下这树第一步旋转的情况，会发现旋转后会右两处不平衡，不过第二次旋转之后就都平衡了）

复习一下，右子树的右节点升高引发的不平衡需要 right-right 旋转。反过来，左子树的左节点升高若是搞不清楚方向，知道这里所说的 right-right 旋转会让目标的地位被它的右节点取代就是了。

右子树的左节点升高需要 right-left。一个 right-left 操作，相当于先对右子树根进行 left-left 旋转，再对最高节点进行 right-right 旋转。

上面这些旋转解决的都是插入（高度升高）引发的不平衡。删除（高度降低）的话实际也差不多，感兴趣的同学可以自己试一下。

4.0 学分的数据结构与算法

我现在又希望课能水一点了。水一点好，水一点学着会轻松很多……